LMNN-基于马氏距离的KNN算法优化

一. 相关背景知识

这篇文章涉及较多的背景知识，包括距离度量，PCA/LDA/RCA等特征提取方法。下面将一一介绍。

1 Distance Metric Learning(距离度量学习)

Metric Learning一直是机器学习中比较重要的一个领域。包括：欧氏距离，马氏距离，曼哈顿距离，Minkowski距离，余弦距离等。相关计算查看附录-1常用的Distance Metric。那么什么样的映射可以称为度量呢? 下面给出定义。

X向量空间中能满足以下性质的映射即可称为度量, 其中满足前三条称为伪度量。:

\begin{align} &1. \ D(x_i,x_j)+ D(x_j,x_k) ≥ D(xi_,x_k)\ (triangular\ inequality). \\ &2. \ D(x_i,x_j) ≥ 0 \ (non-negativity).\\ &3. \ D(x_i,x_j) = D(x_j,x_i)\ (symmetry). \\ &4. \ D(x_i,x_j) = 0 ⇐⇒ x_i =x_j (distinguishability). \end{align}

通过线性变换 \vec x' = L \vec x 后计算欧氏距离，我们可以得到一族度量。L是个满秩的有效的伪度量，其计算如下：

D_L(~x_i,~x_j) = ||L(~x_i −~x_j)||_2^ 2,

当 M = L^TL 时，我们定义广义的Mahalanobis metrics(马氏度量)如下：

D_M(~x_i,~x_ j) = (~x_i −~x_ j)^TM(~x_i −~x_ j)

则当L是实值矩阵时， M一定为半正定矩阵。(也可以将M看做协方差矩阵的逆, 对比马氏距离)

2 Eigenvector Methods(特征向量的方法)

寻找输入空间的信息线性变换 L 时，应用最广泛的是特征向量方法。其中 L 可以看做马氏距离的诱因(M = L^TL)。通用的方法有PCA(主成分分析)，LDA(线性判别分析)，RCA(相关成分分析)。

2.1 PRINCIPAL COMPONENT ANALYSIS(PCA)

PCA的目标是寻找将输入空间投影到方差最大的子空间的线性变换\vec x' = L \vec x，假设原输入空间的协方差矩阵为： C = \frac{1}{n}∑_{i=1}^n (\vec x_i −\vec \mu)^T(\vec x_i −\vec \mu)

则线性变换后的协方差矩阵优化目标为(将 \vec x' = L \vec x 带入上式C中的 x_i ):

\max_a\ L^TCL ,\ s.t \ \ LL^T=I

该目标函数有封闭式的解。标准约定将L的行与协方差矩阵 C 的主要特征向量相等。若L是个矩形矩阵，则变换后维度降低，L若是方形矩阵则维度不变。通常可用特征向量的方式求解。

PCA是无监督方式进行的，没有用到分类问题中的label(标签)信息。PCA可用于“去噪”，将底层特征向量的分量投影出来，可以降低kNN的误差率。也可用于加速大数据集中最近邻的计算。

2.2 LINEAR DISCRIMINANT ANALYSIS(线性判别分析)

LDA是求解一个线性变换\vec x' = L \vec x，使类间方差相对于类内方差最大。这些方差由类间和类内协方差矩阵计算。则类间方差 C_b 和类内方差 C_w 计算如下：

\begin{align} C_b &= \frac{1}{C} \sum_{c=1}^{C} \vec u_c \vec u_c^⊤ \ , \\ C_w &=\frac{1}{n} \sum_{c=1}^{C} \sum_{i∈Ω_C} (\vec x_i −\vec u_c)(\vec x_i −\vec u_c)^T \end{align}

u_c 表示c类的样本均值，假设数据全部中心化。

根据L定义的投影矩阵的约束条件，选择线性变换L来最大化类间方差与类内方差的比值。对于上述协方差矩阵，所需优化如下：

\max_a\ \frac{L^TC_bL}{L^TC_wL} ,\ s.t \ \ LL^T=I

该目标函数的优化有一个封闭式的解。标准惯例把L的行与 C_w^{-1}C_b 的主特征向量相等(可根据广义瑞利商)。

LDA算法的优点：

1）在降维过程中可以使用类间的先验知识经验，PCA为无监督学习，无法使用类间信息

2）LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

LDA算法的缺点：

1）LDA都是基于二阶统计量的(类内和类间方差)，不适合对非多元混合高斯分布样本进行降维；PCA基于所有样本的方差进行统计，同样要求样本为高斯分布。

2）因为类间矩阵 C_b 的秩最多为类别C，LDA的特征工作最多提取C个特征向量。因此降维后的特征最多为C-1个.

3）LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。

4）LDA可能过度拟合数据。

2.3 RELEVANT COMPONENT ANALYSIS(相关成分分析)

在使用标记数据方面，RCA介于PCA和LDA之间。具体来说，RCA利用所谓的“chunklet”信息，或子类成员分配。chunklet本质上是类的子集。同一块块中的输入属于同一类，但不同块中的输入不一定属于不同的类。我们用 \Omega_l 代表属于 l 块的所有样本的集合， \vec u_l 代表 l 块所有样本的均值。总共划分L个子块。则方差计算如下：

C_w =\frac{1}{n} \sum_{l=1}^{L} \sum_{i∈Ω_l} (\vec x_i −\vec u_l)(\vec x_i −\vec u_l)^T

RCA使用线性变换\vec x' = L \vec x， L=C_w^{-1/2} 。这种转变的一个意想不到的副作用可能是放大数据中嘈杂的方向。因此，在计算chunklet内协方差矩阵之前，建议使用PCA去噪。

3 凸优化(特征向量的方法)

距离度量学习的目标可以表示在两个方面:学习一个线性变换\vec x' = L \vec x，或者，学习指标 M =LL^T 。将某些类型的距离度量学习表示为正半定阵M的锥体上的凸优化是可能的。

3.1 MAHALANOBIS METRIC FOR CLUSTERING(马氏距离聚类)

MMC(MAHALANOBIS METRIC FOR CLUSTERING)的目标与上面提到的LDA相似：即最小化label相似的输入之间的距离，同时最大化label不同的输入之间的距离。与LDA不同的是，MMC将距离度量学习问题表示为一个凸优化问题。特别地，LDA通过计算的特征值问题来计算线性变换 L ，而MMC解决了直接表示为马氏度规本身的矩阵 M =LL^T的凸优化。

y_{ij} = 1\ if\ y_i = y_j, and \ y_{i j} = 0\ otherwise。因此MMC算法，最大化不同类别( y_{i j} = 0 )的样本距离和，并约束相同类别的样本( y_{i j} = 1 )的距离和小于等于1. 具体公式如下：

\begin{align} Maximize &∑_{i j}(1− y_{i j})\sqrt{D_M(\vec x_i, \vec x_j) } \\subject to: &(1) ∑_{i j} y_{i j}D_M(\vec x_i, \vec x_j) ≤ 1\\ &(2) M\succeq 0. \end{align}

这是一个QP(quadratic process)问题，第一个约束要求使问题可行且有界，第二个约束条件是M是一个正半定矩阵，使整体优化是凸的。

MMC是为了提高kmeans等迭代聚类算法的性能而设计的，它假设簇为正态分布或单峰分布。试图最小化所有标记相似的输入对之间的距离。而KNN没有隐含地对输入分布做出参数(或其他限制)假设。

3.2 ONLINE LEARNING OF MAHALANOBIS DISTANCES(马氏距离的在线学习)

The Pseudometric Online Learning Algorithm (POLA)伪度量在线学习算法结合了凸优化和大边缘分类(large marge)的思想。与LDA和MMC一样，POLA试图学习一种度量方法，它可以缩短标记相似的输入之间的距离，并扩展标记不同的输入之间的距离。然而，POLA与LDA和MMC的不同之处在于，它明确地鼓励使用有限的边界来分隔不同的标记输入。

POLA尝试学习一个马氏度量M和一个标量阈值b，这样类似标记的输入之间最多只有b-1的距离，而不同标记的输入之间至少有b+1的距离。在时间t，环境呈现元组 (\vec x_t,\vec x_t^′,y_t) 。其中 y_t 为二进制label，当 \vec x_t,\vec x_t^′ 属于相同label时，y_t =1 ；当 \vec x_t,\vec x_t^′ 属于不同的label时， y_t =-1 ；其算法表示如下:

y_t [b−(\vec x_t −\vec x_t^′)^TM(\vec x_t −\vec x_t^′)] ≥ 1.

POLA和MMC有着相同的优势和劣势。这两种算法都基于凸优化，不存在伪局部极小值。两种算法都对输入和类标签的分布做了隐含的假设。POLA强制的边界约束是为了学习一个距离度量，在这个度量下，所有标记相似的输入对都比所有标记不同的输入对更近。

3.3 Neighborhood Component Analysis(邻域成分分析NCA)

NCA是一种监督学习算法, NCA中的随机分类器是通过附近训练实例的多数投票来标记查询，但不一定是k个最近邻。NCA对于不同样本之间定义了一个softmax概率：

p_{i j} = \begin{cases} \frac{\exp{(-||\bm Lx_i-\bm Lx_j||^2})}{\sum_{k\ne i}{\exp{(-||\bm Lx_i-\bm Lx_k||^2})}} & \text{if } i \ne j \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 & \text{if } i=j \end{cases}\\

损失函数定义如下，其中 y_{ij} = 1\ if\ y_i = y_j, and \ y_{i j} = 0\ otherwise。

ε_{NCA} = 1− \frac{1}{n} ∑_{ij}p_{i j}y_{i j}.

虽然距离度量的参数是连续可微的，但上式不是凸的，也不能用特征向量方法最小化。因此，NCA中的优化可能存在伪局部极小值。

二. LMNN模型搭建

1 模型构建

LMNN模型源自两个直觉：1> 每个训练输入 \vec x_i 应该与它的k个近邻样本拥有相同的balel y_i ;2> 不同label的样本在训练时应该被广泛分开。

作者定义了impostors(伪装者)的概念(见附图)，即拥有不同label的impostors( \vec x_l)侵入到由单位margin和 \vec x_i 的目标邻居组成的边界内 。假设对任意根本(\vec x_i， y_i) ， \vec x_j 与 \vec x_i 有相同的label， \vec x_l 与 \vec x_i 有不同的label( y_l \ne y_i )。则impostors满足以下公式：

\left\|\mathbf{L}\left(\vec{x}_{i}-\vec{x}_{l}\right)\right\|^{2} \leq\left\|\mathbf{L}\left(\vec{x}_{i}-\vec{x}_{j}\right)\right\|^{2}+1

损失函数定义分为两个， \varepsilon_{pull} 和 \varepsilon_{push}，分别对应前面提到的两个直觉。我们定义 j \leadsto i 为\vec x_j 是\vec x_i的目标邻居，y_{il} = 1\ if\ y_i = y_l, and \ y_{i l} = 0\ otherwise。

则\varepsilon_{pull} 的损失函数：

\varepsilon_{\text {pull }}(\mathbf{L})=\sum_{j \leadsto i}\left\|\mathbf{L}\left(\vec{x}_{i}-\vec{x}_{j}\right)\right\|^{2}

同时\varepsilon_{push}的损失函数，其中 [z]+ = max(z,0) 代表标准的hinge loss损失：

\varepsilon_{\text {push }}(\mathbf{L})=\sum_{i, j \leadsto i} \sum_{l}\left(1-y_{i l}\right)\left[1+\left\|\mathbf{L}\left(\vec{x}_{i}-\vec{x}_{j}\right)\right\|^{2}-\left\|\mathbf{L}\left(\vec{x}_{i}-\vec{x}_{l}\right)\right\|^{2}\right]_{+}

最后合并的损失函数：

\varepsilon(\mathbf{L})=(1-\mu) \varepsilon_{p u l l}(\mathbf{L})+\mu \varepsilon_{p u s h}(\mathbf{L}) (13)

文中提到u取0.5即可，通过实验验证分类效果对u的取值不敏感。

作者一个小实验对算法有效性进行验证。结果如上图，并得到如下结论：

LMNN 仅仅会对不同于当前label的“邻近”距离最大的几个点进行“推”操作，而不会对所（全局）有的样本都进行操作。而LDA，RCA，和MCC会对“所有”样本采用这种，操作。这反而会增加大的KNN分类中的错误。

2 凸优化

上式(13)中的损失函数在线性变换L的矩阵元素中不是凸的。

为了使损失函数最小化，一种直接的方法是L元素的梯度下降，但是这种方法容易陷入局部极小。我们对损失函数的线性变换的距离用马氏距离表示，则有：

\varepsilon(\mathbf{M})=(1-\mu) \sum_{i, j \leadsto i} \mathcal{D}_{\mathbf{M}}\left(\vec{x}_{i}, \vec{x}_{j}\right)+\mu \sum_{i, j \leadsto i} \sum_{l}\left(1-y_{i l}\right)\left[1+\mathcal{D}_{\mathbf{M}}\left(\vec{x}_{i}, \vec{x}_{j}\right)-\mathcal{D}_{\mathbf{M}}\left(\vec{x}_{i}, \vec{x}_{l}\right)\right]_{+} \ \ \ (14)

很显然新的损失函数是一个基于半正定矩阵限制条件的凸优化问题(semidefinite programming SDP)。

因为有时候不一定能严格满足上述的那种条件，因此引入一个非负松弛变量 \xi_{i j l} ，可以得到：

\begin{array}{l}{\text { Minimize }(1-\mu) \sum_{i, j \leadsto i}\left(\vec{x}_{i}-\vec{x}_{j}\right)^{\top} \mathbf{M}\left(\vec{x}_{i}-\vec{x}_{j}\right)+\mu \sum_{i, j\leadsto i, l}\left(1-y_{i l}\right) \xi_{i j l} \\\text { subject to: }} \\ {\text { (1) }\left(\vec{x}_{i}-\vec{x}_{l}\right)^{\top} \mathbf{M}\left(\vec{x}_{i}-\vec{x}_{l}\right)-\left(\vec{x}_{i}-\vec{x}_{j}\right)^{\top} \mathbf{M}\left(\vec{x}_{i}-\vec{x}_{j}\right) \geq 1-\xi_{i j l}} \\ {\text { (2) } \xi_{i j l} \geq 0} \\ {\text { (3) } \mathbf{M} \succeq 0}\end{array}

3 基于能量分类

基于Mahalabonis Metric的矩阵M可用于KNN算法来解决分类问题，也可以直接使用损耗函数作为所谓的“基于能量的”分类器。

将一个测试样本作为一个额外的训练样本进行能量分类，并对每个可能的label y_{t}计算Eq.(14)中的损耗函数。对于一个测试样本 \vec{x}_{t} 和它所对应的标签 y_{t} ，计算相应的损失。损失共包含三项：前两项分别对应上文中式（14）中的两项，第三项，增加了\vec{x}_{t}样本作为其他样本的伪装者时的损失。最后测试样本的类别能根据以下等式得到：

\begin{equation} \left.{}{y_{t}=\operatorname{argmin}_{y_{t}}\left\{(1-\mu) \sum_{j \leadsto t} \mathcal{D}_{\mathbf{M}}\left(\vec{x}_{t}, \vec{x}_{j}\right)+\mu \sum_{j \leadsto t, l}\left(1-y_{t l}\right)\left[1+\mathcal{D}_{\mathbf{M}}\left(\vec{x}_{t}, \vec{x}_{j}\right)-\mathcal{D}_{\mathbf{M}}\left(\vec{x}_{t}, \vec{x}_{l}\right)\right]_{+}\right.} {} \\ {+\mu \sum_{i, j \leadsto i}\left(1-y_{i t}\right)\left[1+\mathcal{D}_{\mathbf{M}}\left(\vec{x}_{i}, \vec{x}_{j}\right)-\mathcal{D}_{\mathbf{M}}\left(\vec{x}_{i}, \vec{x}_{t}\right)\right]_{+}}\right\} \end{equation}

三 实验结果

实验中评估了九个不同大小和难度的数据集的LMNN分类。其中一些数据集来自于图像、语音和文本的集合，产生了非常高维的输入，针对这些使用了PCA来减少训练前输入的维数。

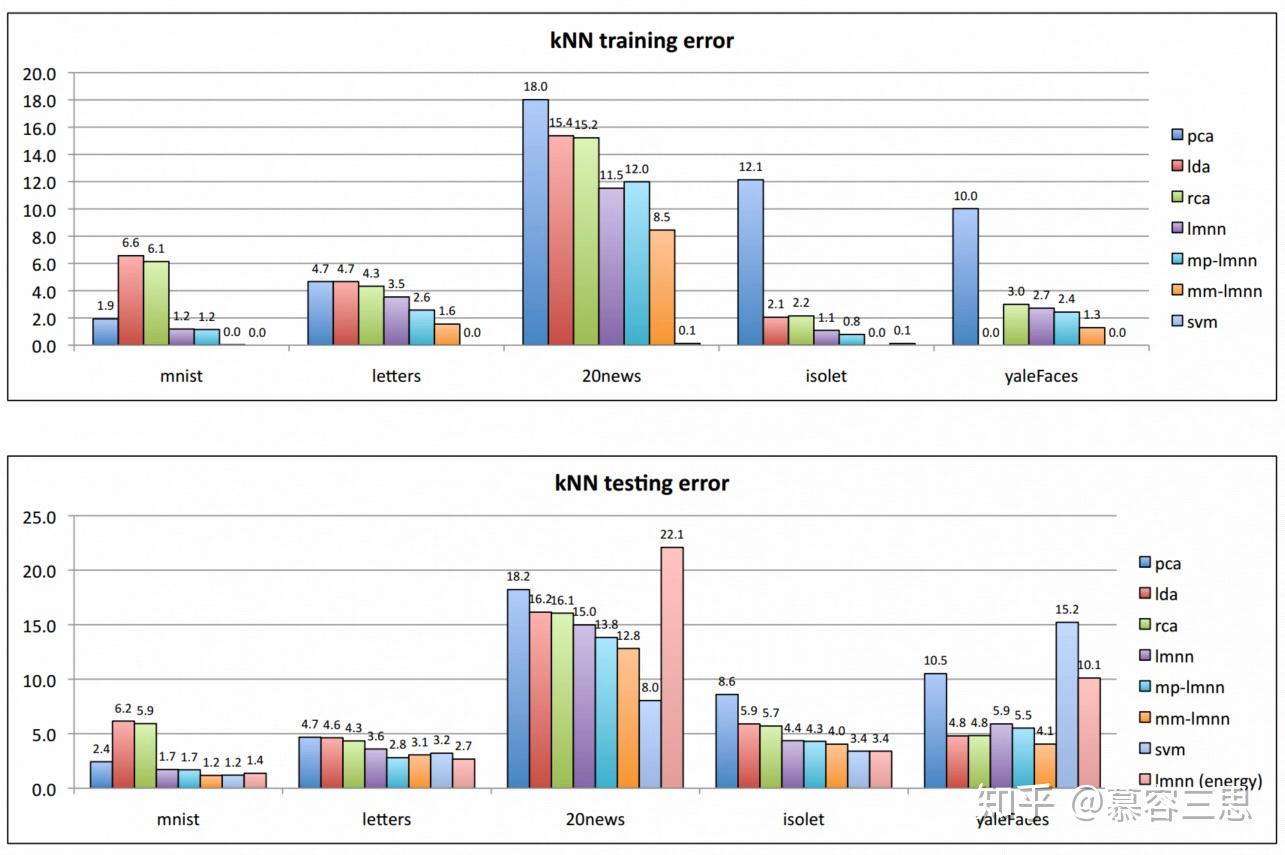
实验结果如下：

1）使用了Mahalanobis距离以后的KNN明显性能优于欧几里得距离的KNN，无论是在训练集还是测试集上。

2）使用'基于能量的分类'的trick会使结果在LMNN分类的基础上有进一步提升。(但图中的数据显示只有minist, letters和isolet三个数据集上有少量的提升)

3) 当预处理需要降维时，PCA比LDA更有效.

4) LMNN分类对更大的数据集有更好的改进;

5) 对比SVM的结果，energy-based LMNN分类算法与SVM水平相当。在20news训练集LMNN效果明显比SVM差，主要是因为SVM使用原始的20000维的特征进行训练，而LMNN仅使用200维的主成分特征进行训练。

作者分别对多个小数据集进行实验，数据集分别为：minist(手写数字识别), letters(字母识别), 20news(新闻分类), isolet(语音识别), yFaces(人脸识别)。 验证结果如下表。

四 拓展

4.1 Multi-pass LMNN

LMNN的一个潜在缺点是必须预先指定目标邻居。在缺乏先验知识的情况下，默认的选择是使用欧几里德距离来确定目标近邻。目标近邻在学习过程中是固定的，而实际近邻可能由于输入空间的线性变换而发生变化。

这里采用迭代的方式，通过每次训练的Mahalanobis的L矩阵，并根据欧几里得距离来确定邻近样本。\vec{x}_{i} \rightarrow \mathbf{L}_{p} \mathbf{L}_{p-1} \ldots \mathbf{L}_{1} \mathbf{L}_{0} \vec{x}_{i}\left(\text { with } \mathbf{L}_{0}=\mathbf{I}\right)

4.2 Multi-metric LMNN

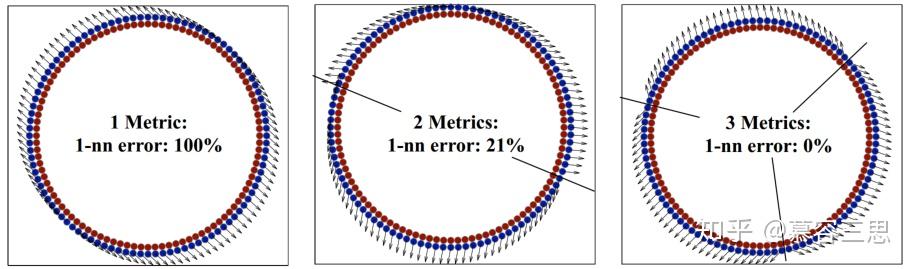
在某些数据集上，输入空间的全局线性变换可能不足以改进kNN分类。显示了一个合成数据集的示例，对于该数据集，单一度量是不够的。数据集由两个同心圆采样的输入组成，每个同心圆定义一个不同的类成员。全局线性变换并不能提高该数据集的kNN分类精度。通常，一个单一的马氏距离度量不能很好地模拟高度非线性的多类决策边界。

因此我们采用了根据样本来训练多个局部的Mahalanobis Metrix变换矩阵。

根据K-means将训练数据进行分割类聚。然后对每个Cluster训练一个局部的Mahalanobis metric，

\hat{\mathcal{D}}\left(\vec{x}_{i}, \vec{x}_{j}\right)=\left(\vec{x}_{i}-\vec{x}_{j}\right)^{\top} \mathbf{M}^{y_{j}}\left(\vec{x}_{i}-\vec{x}_{j}\right)

解决以下的优化问题：

\begin{array}{l}{\text { Minimize }(1-\mu) \sum_{i, j \leadsto i}\left(\vec{x}_{i}-\vec{x}_{j}\right)^{\top} \mathbf{M}^{y_{j}}\left(\vec{x}_{i}-\vec{x}_{j}\right)+\mu \sum_{j \leadsto i, l}\left(1-y_{i l}\right) \xi_{i j l}} \\ {\text { subject to: }} \\ {\text { (1) }\left(\vec{x}_{i}-\vec{x}_{l}\right)^{\top} \mathbf{M}^{y_{l}}\left(\vec{x}_{i}-\vec{x}_{l}\right)-\left(\vec{x}_{i}-\vec{x}_{j}\right)^{\top} \mathbf{M}^{y_{j}}\left(\vec{x}_{i}-\vec{x}_{j}\right) \geq 1-\xi_{i j l}} \\ {\text { (2) } \xi_{i j l} \geq 0} \\ {\text { (3) } \mathbf{M}^{i} \succeq 0 \text { for } i=1, \ldots, c}\end{array}

4.3 Kernel Version

LMNN也可以通过使用内核方法扩展到一个非线性特征空间，而不是原始的输入空间。

\mathbf{K}_{i j}=\Phi\left(\vec{x}_{i}\right)^{\top} \Phi\left(\vec{x}_{j}\right)

则马氏度量M： \mathbf{M}=\sum_{l m} \mathbf{A}_{l m} \Phi\left(\vec{x}_{l}\right) \Phi\left(\vec{x}_{m}\right)^{\top}

4.4 降维方法

根据训练出来的方阵L，取他的主特征（特征值最大的特征向量）构建映射矩阵P，原数据就可以通过映射矩阵进行降维。

或者构建一个尺寸为rxd的L矩阵，r是想要降维后的维度，直接训练出L，但这就不是一个凸优化问题了。

五 Ball Trees

作者还提出了Ball Trees思想来提升算法速度，这里不做介绍。

六 总结

这篇文章主要涉及到度量学习的相关内容，将SVM的margin思想应用到KNN算法，本文使用马氏度量学习，通过使相同label样本距离更近 ，不同label的样本距离更远(仅考虑k个临近样本)，的思想构建损失函数，求解相应的距离度量L。本文的算法设计十分巧妙。

附录：

1 常用的Distance Metric

假设 X, Y 分别为特征长度为n的点的向量表示.

1> Euclidian distance(欧式距离)：

dist(X, Y) = || X-Y||^2_2 = \sqrt{\sum_{i=1}^{n}{|x_i - y_i|^2}}

2> Manhattan distance(曼哈顿距离) / Absolute distance(绝对值距离):

dist(X, Y) = || X-Y|| = \sum_{i=1}^{n}{|x_i - y_i|}

3> Minkowski distance(闵可夫斯基距离)

dist(X, Y) = || X-Y||^p_p = (\sum_{i=1}^{n}{|x_i - y_i|^p})^{\frac{1}{p}}

Minkowski距离是欧式距离和Manhattan距离的更广义的拓展.

4> Chebyshev distance(切比雪夫距离)

dist(X, Y) =\max_{i=1}^{n}{|x_i - y_i|}

当 p\rightarrow\infty 时的Minkowski距离就是Chebyshev距离.

5> Mahalanobis distance(马氏距离)

马氏距离可以度量一个点与一个分布之间的距离，也可以用来度量同一分布下两个点的距离。它主要是在欧氏距离的基础上增加了协方差矩阵的考量，

假设m个样本组成了一个分布，每个样本的特征维度是n。其中列向量向\vec x_1, ..., \vec x_m代表m个样本，行向量 \vec X_1, ..., \vec X_n 代表n个特征的分布向量。

\begin{align} X_{m\times n} &=\left[\begin{array} {cccc} \vec x_{1}\ , \vec x_{2} \ , \vec x_{3} \ ,{\cdots} \ , \vec x_{m} \end{array}\right] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\&=\left[\begin{array} {cccc} x_{11} & x_{21} & {\cdots} & x_{m1} \\ x_{12} & x_{22} & {\cdots} & x_{m2} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ x_{1n} & x_{2n} & {\cdots} & x_{mn} \end{array} \right] =\left[\begin{array} {cccc} \vec X_{1} \\ \vec X_{2} \\ {\vdots}\\ \vec X_{n} \end{array} \right] \end{align}

则m个样本的均值向量为，\vec {u}= \left[\begin{array} {cccc} \vec u_{1} \\ \vec u_{2} \\ {\vdots}\\ \vec u_{n} \end{array} \right]

则定义协方差矩阵 S 和对应计算如下:

\begin{align} S &=\left[\begin{array} {cccc} cov(\vec X_1,\vec X_1) & cov(\vec X_1,\vec X_2) & {\cdots} & cov(\vec X_1,\vec X_n) \\ cov(\vec X_2,\vec X_1) & cov(\vec X_2,\vec X_2) & {\cdots} & cov(\vec X_2,\vec X_n) \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ cov(\vec X_n,\vec X_1) & cov(\vec X_n,\vec X_2) & {\cdots} & cov(\vec X_n,\vec X_n) \\ \end{array} \right] \\ \\ &=\left[\begin{array} {cccc} E(\vec X_1-u_1)(\vec X_1-u_1) & E(\vec X_1-u_1)(\vec X_2-u_2) & {\cdots} & E(\vec X_1-u_1)(\vec X_n-u_n)\\ E(\vec X_2-u_2)(\vec X_1-u_1)&E(\vec X_2-u_2)(\vec X_2-u_2) & {\cdots} &E(\vec X_2-u_2)(\vec X_n-u_n) \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ E(\vec X_n-u_n)(\vec X_1-u_1)&E(\vec X_n-u_n)(\vec X_2-u_2) & {\cdots} &E(\vec X_n-u_n)(\vec X_n-u_n) \\ \end{array} \right] \\ \\ &=\left[\begin{array} {cccc} \sum_{i=1}^{m}{(x_{m1}-u_1)^2} & \sum_{i=1}^{m}{(x_{m1}-u_1)(x_{m2}-u_2)} & {\cdots} & \sum_{i=1}^{m}{(x_{m1}-u_1)(x_{mn}-u_n)} \\ \sum_{i=1}^{m}{(x_{m2}-u_2)(x_{m1}-u_1)} & \sum_{i=1}^{m}{(x_{m2}-u_2)^2} & {\cdots} & \sum_{i=1}^{m}{(x_{m2}-u_2)(x_{mn}-u_n)} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ \sum_{i=1}^{m}{(x_{mn}-u_n)(x_{m1}-u_1)} & \sum_{i=1}^{m}{(x_{mn}-u_n)(x_{m2}-u_2)} & {\cdots} & \sum_{i=1}^{m}{(x_{mn}-u_n)^2} \\ \end{array} \right] \\ \end{align}\\

则对于一个均值为 \vec {u} , 协方差矩阵为 S , 的多变量矢量样本 \vec x_{i} , 其马氏距离为

D_M(\vec {x_i}) = \sqrt{(\vec {x_i} - \vec {u})^T S^{-1}(\vec {x_i} - \vec {u})}

当两个矢量样本\vec x_{i}, \vec x_{j}均属于该分布时, 二者的马氏距离:

D_M(\vec {x_i},\vec {x_j}) = \sqrt{(\vec {x_i} - \vec {x_j})^T S^{-1}(\vec {x_i} - \vec {x_j})}

6> cosin余弦相似度距离:

dist(X, Y) = \frac{X\cdot Y}{||X||\cdot||Y||}

7> Jaccard distance(杰卡德距离)

主要用来评估两个集合A, B之间的距离

dist(A, B) = \frac{A \cap B}{A\cup B}

8> hamming distance(汉明距离)

比较两个二进制的数，对应位不同的bit的数量。

比如：1011101 与 1001001 之间的汉明距离是 2

9> kernal distance(核函数距离)

dist(X, Y) = || \Phi (X)-\Phi (Y)||^2_2 ( \Phi 为kernal函数)