极化码的入门与探索

极化码的基础先验知识

二进制输入离散无记忆信道模型(Binary-input Discreten Memoryless Channel, B-DMC)

给定B-DMC信道$W:\mathcal{X}\to \mathcal{Y}$，信道转移概率(transition probability)为$W(y|x),x\in \mathcal{X},y\in y$。对于B-DMC信道而言，输入信号的集合一般为 X = { 0 , 1 } \mathcal X=\{0,1\} X={0,1}，输出信号集合$\mathcal{Y}$和转移概率$W(y|x)$具有任意形式。

We write $W^N$ to denote the channel correpsonding to $N$ use of $W$, thus, $W^N:{\mathcal{X}}^N\to {\mathcal{Y}}^N$ with $W^N(x_1^N|y_1^N)={\prod }_{i=1}^{N}W(y_i|x_i)$.
The symmetric capacity is the highest rate achievable subject to using the input letters of the channel with equal probability.

二进制离散输入信道的ML判决和错误率

二进制输入离散信道$W$的最大似然（ML）判决指当收到符号$y$时，$x$的值按下式判决
ML判决准则
x ^ M L = arg max ⁡ x ∈ { 0 , 1 } W ( y ∣ x ) \hat x_{ML} = \argmax_{x \in \{0,1\}} W(y|x) x^ML​=x∈{0,1}argmax​W(y∣x)

ML判决的错误率的两种等价写法
P e M L ( W ) = 1 2 ∑ y ∈ Y min ⁡ { W ( y ∣ 0 ) , W ( y ∣ 1 ) } P e M L ( W ) = ∑ x , y 1 2 W ( y ∣ x ) 1 { W ( y ∣ x ) ≤ W ( y ∣ x ⊕ 1 ) } ( x , y ) \begin{aligned} P^{ML}_e(W) &= \frac{1}{2} \sum_{y \in \mathcal Y} \min \left \{W(y|0), W(y|1) \right \} \\ P^{ML}_e(W) &=\sum_{x, y} \frac{1}{2} W(y|x) \mathbb 1_{ \{ W(y|x) \leq W(y | x \oplus 1) \} } \left ( x, y \right) \end{aligned} PeML​(W)PeML​(W)​=21​y∈Y∑​min{W(y∣0),W(y∣1)}=x,y∑​21​W(y∣x)1{W(y∣x)≤W(y∣x⊕1)}​(x,y)​

对错误率表达式的简单理解：

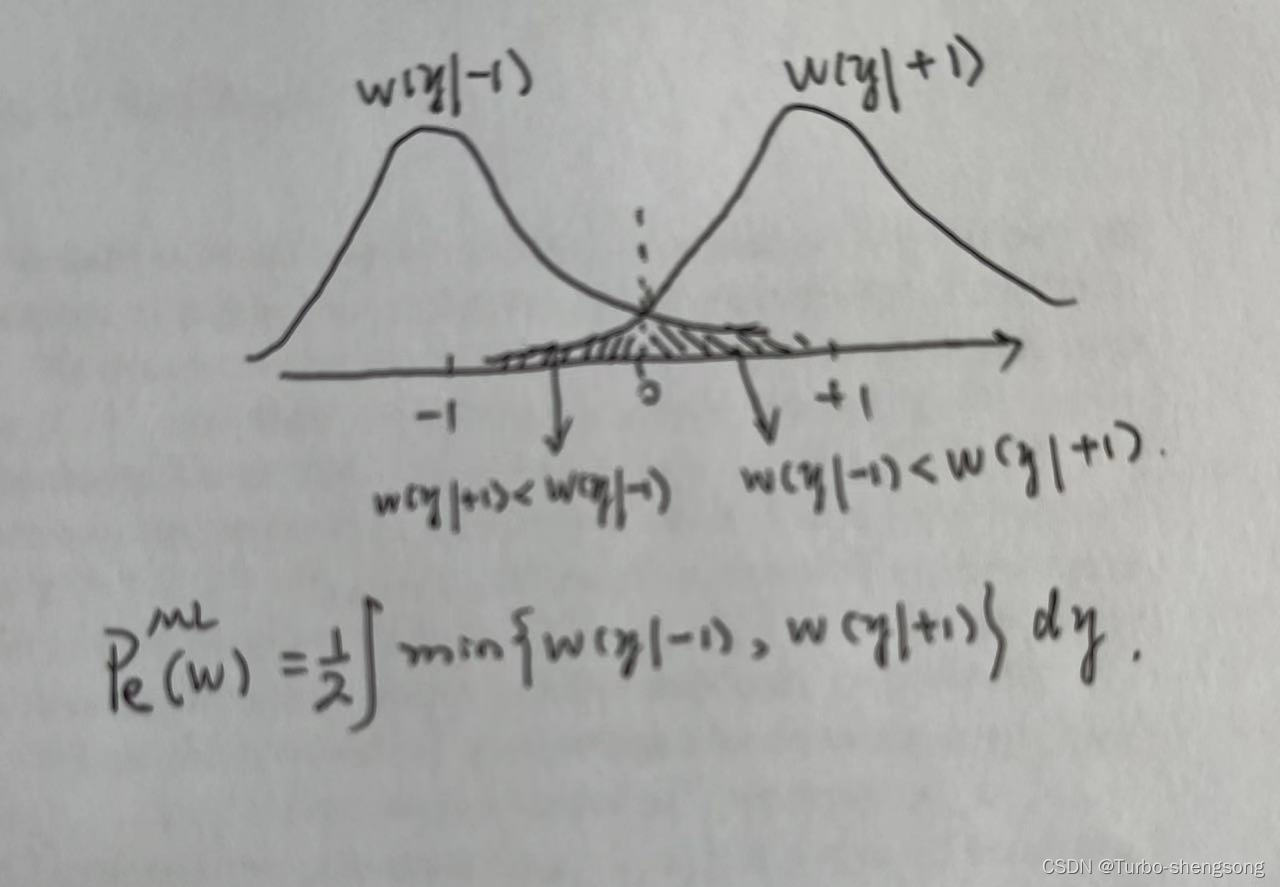
B-DMC相关参数的定义和理解

对于B-DMC信道$W:\mathcal{X}\to \mathcal{Y}$，相应的信道互信息(or say, symmetric capacity)、差错概率与Bhattacharyya参数（简称巴氏参数）分别定义为：
I ( W ) ≜ ∑ y ∈ Y ∑ x ∈ X 1 2 W ( y ∣ x ) log ⁡ W ( y ∣ x ) 1 2 W ( y ∣ 0 ) + 1 2 W ( y ∣ 1 ) P e ( W ) ≜ ∑ x , y 1 2 W ( y ∣ x ) 1 { W ( y ∣ x ) ≤ W ( y ∣ x ⊕ 1 ) } ( x , y ) Z ( W ) ≜ ∑ y ∈ Y W ( y ∣ 0 ) W ( y ∣ 1 ) \begin{aligned} I(W) & \triangleq \sum_{y \in \mathcal Y} \sum_{x \in \mathcal X} \frac{1}{2} W(y|x) \log \frac{W(y|x)}{ \frac{1}{2} W(y|0) + \frac{1}{2} W(y|1) } \\ P_e(W) & \triangleq \sum_{x, y} \frac{1}{2} W(y|x) \mathbb 1_{ \{ W(y|x) \leq W(y | x \oplus 1) \} } \left ( x, y \right) \\ Z(W) & \triangleq \sum_{y \in \mathcal Y} \sqrt { W(y|0) W(y|1) } \end{aligned} I(W)Pe​(W)Z(W)​≜y∈Y∑​x∈X∑​21​W(y∣x)log21​W(y∣0)+21​W(y∣1)W(y∣x)​≜x,y∑​21​W(y∣x)1{W(y∣x)≤W(y∣x⊕1)}​(x,y)≜y∈Y∑​W(y∣0)W(y∣1) ​​

这里我们证明$P_e(W)\le Z(W)$，即巴氏参数$Z(W)$是ML判决差错概率的上界

证明：$P_e(W)\le Z(W)$
min ⁡ { W ( y ∣ 0 ) , W ( y ∣ 1 ) } ≤ W ( y ∣ 0 ) W ( y ∣ 1 ) \min \left \{W(y|0), W(y|1) \right \} \leq \sqrt { W(y|0) W(y|1) } min{W(y∣0),W(y∣1)}≤W(y∣0)W(y∣1) ​
即可得证。

进一步解释$I(W)$和$Z(W)$的物理意义

• 互信息$I(W)$衡量B-DMC信道W的可达速率，即输入信号先验等概条件下可靠通信的最高数据率。
• 巴氏参数$Z(W)$表示信道$W$发送比特0或1，采用最大似然判决准则的差错概率上界。

对于B-DMC信道而言，$I(W),Z(W)\in [0,1]$。

从直观上讲，我们希望$I(W)\approx 1$ iff $Z(W)\approx 0$； $I(W)\approx 0$ iff $Z(W)\approx 1$，下面将给出相关的证明。

Proposition 1: 对任意B-DMC $W$，有
$$\begin{array}{rl}I(W)& \ge \log \frac{2}{1+Z(W)}\\ I(W)& \le \sqrt{1-Z(W{)}^2}\end{array}$$

证明(Prop. 1)：
Proof of $I(W)\ge \log \frac{2}{1+Z(W)}$: 省略。
Proof of $I(W)\le \sqrt{1-Z(W{)}^2}$：
对于B-DMC信道$W:\mathcal{X}\to \mathcal{Y}$，我们首先定义
$$d(W)\triangleq \frac{1}{2}\sum _{y\in \mathcal{Y}}\left|W(y|0)-W(y|1)\right|$$

$d(W)$表示两个关于$y$的分布$W(y|0)$和$W(y|1)$之间的变分距离(Variational Distance)。
引理-1：对任意B-DMC信道$W:\mathcal{X}\to \mathcal{Y}$，$I(W)\le d(W)$
Proof of 引理-1：令$W$是任意的B-DMC，其输出的集合为 Y = { 1 , ⋯   , n } \mathcal Y=\{1,\cdots,n\} Y={1,⋯,n}，且令$P_i=W(i|0),Q_i=W(i|1),i=1,2,\cdots ,n$，那么根据定义，我们有
$$I(W)=\sum _{i=1}^n\frac{1}{2}\left[P_i\log \frac{P_i}{\frac{1}{2}{P}_i+\frac{1}{2}{Q}_i}+Q_i\log \frac{Q_i}{\frac{1}{2}{P}_i+\frac{1}{2}{Q}_i}\right]$$

对于上式$[\cdot ]$中的内容，我们可以定义
$$f(x)\triangleq x\log \frac{x}{x+\delta }+(x+2\delta )\log \frac{x+2\delta }{x+\delta }$$

其中 x = min ⁡ { P i , Q i } x=\min\{P_i, Q_i\} x=min{Pi​,Qi​}，$\delta =\frac{1}{2}|P_i-Q_i|$。我们考虑在$0\le x\le 1-2\delta$的区间内最大化$f(x)$，计算
$$\frac{df}{dx}=\frac{1}{2}\log \frac{\sqrt{x(x+2\delta )}}{x+\delta }$$

注意到，上述表达式的分子$\sqrt{x(x+2\delta )}$和分母$(x+\delta )$，分别对应两个正数$x$和$(x+2\delta )$的几何平均(geometric mean)和算数平均(arithmetic mean)，因此$df/dx\le 0$，当$x=0$时，$f(x)$取最大，所以$f(x)\le f(0)=2\delta$，对应的互信息满足：
$$I(W)\le \sum _{i=1}\frac{1}{2}|P_i-Q_i|=d(W)$$

引理-2：对任意B-DMC信道$W:\mathcal{X}\to \mathcal{Y}$，$d(W)\le \sqrt{1-Z(W{)}^2}$
证明从略。

因此可以得到$I(W)\le \sqrt{1-Z(W{)}^2}$

对称信道(symmetric channel)：对于B-DMC信道$W$，假设存在重排变换$\pi$，对于输出信号集合$\mathcal{Y}$，满足如下两个条件：
(1) 重排变换可逆：${\pi }^{-1}=\pi$
(2) 对于任意的$y\in \mathcal{Y}$，$W(y|1)=W(\pi (y)|0)$
则称B-DMC信道$W$满足对称性。（由经典信息论可知，对于对称信道$W$，它的互信息等于信道容量，即$I(W)=C$）

这里列举两种常用的对称信道
example-1: 二元对称信道(BSC) W : X = { 0 , 1 } → Y = { 0 , 1 } W: \mathcal X=\{0,1\} \rightarrow \mathcal Y=\{0,1\} W:X={0,1}→Y={0,1}，其满足对称性，即
$$\begin{array}{rl}W(0|0)& =W(1|1)\\ W(1|0)& =W(0|1)\end{array}$$

example-2：二元删余信道(BEC) W : X = { 0 , 1 } → Y = { 0 , e , 1 } W: \mathcal X=\{0,1\} \rightarrow \mathcal Y=\{0,e,1\} W:X={0,1}→Y={0,e,1}（$e$是删除符号），也满足对称性，即
$$\begin{array}{rl}W(0|0)& =W(1|1)\\ W(e|0)& =W(e|1)\end{array}$$

其中$\pi (0)=1,\pi (1)=0,\pi (e)=e$。

符号的定义
我们定义$a_1^N$表示行向量$(a_1,\cdots ,a_N)$，给定行向量$a_1^N$，我们记$a_i^j$为子向量$(a_i,\cdots ,a_j),1\le i\le j\le N$。给定$a_1^N$和集合 A ⊂ { 1 , ⋯   , N } \mathcal A \subset \{1, \cdots, N\} A⊂{1,⋯,N}，我们用$a_{\mathcal{A}}$来指定子向量$(a_i,i\in \mathcal{A})$。我们记$a_{1,o}^j$来指明奇数索引(odd indices) $(a_k,1\le k\le j;k\text{ odd})$，类似地，记$a_{1,e}^j$来指明偶数索引(even indices) $(a_k,1\le k\le j;k\text{ even})$。

两信道极化

首先给出一个二元删余信道(BEC)的两信道极化示例，如下图所示

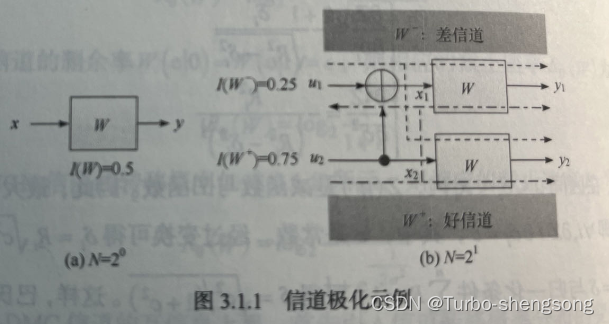
图(a)给出了删余率$ϵ=0.5$的BEC信道的映射关系 W : X = { 0 , 1 } → Y = { 0 , e , 1 } W: \mathcal X=\{0,1\} \rightarrow \mathcal Y=\{0, e, 1\} W:X={0,1}→Y={0,e,1}，其信道互信息为$I(W)=0.5$，巴氏参数$Z(W)=0.5$。

图(b)是2信道极化的过程， u 1 , u 2 ∈ { 0 , 1 } u_1,u_2 \in \{0,1\} u1​,u2​∈{0,1}是输入信道的两比特， x 1 , x 2 ∈ { 0 , 1 } x_1, x_2 \in \{0,1\} x1​,x2​∈{0,1}是经过模2加编码后的两比特，将其分别送入信道$W$后得到$y_1,y_2\in \mathcal{Y}$两个输出信号。对应的编码过程为
$$(x_1,x_2)=(u_1,u_2)\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]=(u_1,u_2){\mathbf{F}}_2$$

通过矩阵${\mathbf{F}}_2$的极化操作，将一对独立信道$(W,W)$变换为两个相关的子信道$(W^{-},W^{+})$，其中

• $W^{-}:\mathcal{X}\to {\mathcal{Y}}^2$ (信道的输入输出关系对应上图中的虚线)
• $W^{+}:\mathcal{X}\to {\mathcal{Y}}^2\times \mathcal{X}$(信道的输入输出关系对应上图中的点划线)

两个子信道的互信息满足下面的关系：
$$\begin{array}{rl}I(W^{-})& \le I(W)\le I(W^{+})\\ Z(W^{-})& \ge Z(W)\ge Z(W^{+})\end{array}$$

由于$I(W^{-})\le I(W^{+})$，这两个子信道产生了分化，$W^{+}$是好信道，$W^{-}$是差信道，这就是极化现象。我们称矩阵${\mathbf{F}}_2$为$2\times 2$的极化核（或称为二阶极化核）

对于一般的B-DMC信道$W$，两信道极化是普遍存在的，有如下定理：

定理1：对于两信道极化变换$(W,W)\mapsto (W^{-},W^{+})$，相应的极化子信道互信息满足：
$$\begin{array}{rl}I(W^{-})& +I(W^{+})=2I(W)\\ I(W^{-})& \le I(W)\le I(W^{+})\end{array}$$
当且仅当$I(W)=0,1$时，等号成立。

证明：给定B-DMC信道$W:\mathcal{X}\to \mathcal{Y}$，经过两信道极化变换$(u_1,u_2)\to (u_1\oplus u_2,u_2)=(x_1,x_2)$，得到的复合信道$W\times W:{\mathcal{X}}^2\to {\mathcal{Y}}^2$分解为两个极化子信道$W^{-}:\mathcal{X}\to {\mathcal{Y}}^2$与$W^{+}:\mathcal{X}\to {\mathcal{Y}}^2\times \mathcal{X}$。

复合信道$W\times W$的转移概率为
$$\begin{array}{rl}W(y_1,y_2|u_1,u_2)& =W(y_2|u_2)W(y_1|u_2\oplus u_1)\\ & =W(y_2|x_2)W(y_1|x_1)\end{array}$$

对于极化子信道$W^{-}:\mathcal{X}\to {\mathcal{Y}}^2$，转移概率为
$$\begin{array}{rl}{W}_2^{(1)}(y_1,y_2|u_1)& =\frac{{\sum }_{u_2=0}^{1}P(y_1,y_2,u_1,u_2)}{P(u_1)}\\ & =\frac{{\sum }_{u_2=0}^{1}P(u_1)P(u_2)W(y_1,y_2|u_1,u_2)}{P(u_1)}\\ & =\sum _{u_2=0}^1\frac{1}{2}W(y_1,y_2|u_1,u_2)\\ & =\sum _{u_2=0}^1\frac{1}{2}W(y_2|u_2)W(y_1|u_2\oplus u_1)\end{array}$$

对于极化子信道$W^{+}:\mathcal{X}\to {\mathcal{Y}}^2\times \mathcal{X}$，转移概率为
$$\begin{array}{rl}{W}_2^{(2)}(y_1,y_2,u_1|u_2)& =\frac{P(y_1,y_2,u_1,u_2)}{P(u_2)}\\ & =\frac{1}{2}W(y_1,y_2|u_1,u_2)\\ & =\frac{1}{2}W(y_2|u_2)W(y_1|u_2\oplus u_1)\end{array}$$

根据互信息链式法则：
$$I(U_1,U_2;Y_1,Y_2)=I(U_1;Y_1,Y_2)+I(U_2;Y_1,Y_2|U_1)$$

我们不难发现，$I(U_1;Y_1,Y_2)$就是极化子信道$W^{-}$的互信息，$I(U_2;Y_1,Y_2|U_1)$的条件互信息为：
$$\begin{array}{rl}I(U_2;Y_1,Y_2|U_1)& =\sum _{y_1,y_2}\sum _{u_1,u_2}P(y_1,y_2,u_1,u_2)\log \frac{P(y_1,y_2|u_1;u_2)}{P(y_1,y_2|u_1)P(u_2)}\\ & =\sum _{y_1,y_2}\sum _{u_1,u_2}P(y_1,y_2,u_1,u_2)\log \frac{P(y_1,y_2|u_1,u_2)}{P(y_1,y_2|u_1)}\\ & =\sum _{y_1,y_2}\sum _{u_1,u_2}P(y_1,y_2,u_1,u_2)\log \frac{P(y_1,y_2,u_1|u_2)\cdot \frac{P(u_2)}{P(u_1)P(u_2)}}{\frac{P(y_1,y_2,u_1)}{P(u_1)}}\\ & =\sum _{y_1,y_2}\sum _{u_1,u_2}P(y_1,y_2,u_1,u_2)\log \frac{P(y_1,y_2,u_1|u_2)}{P(y_1,y_2,u_1)}\\ & =I(U_2;Y_1,Y_2,U_1)=I(W^{+})\end{array}$$

代入到链式法则中，可以得到$I(U_1,U_2;Y_1,Y_2)=I(W^{-})+I(W^{+})$。

另外，因为
$$I(U_1,U_2;Y_1,Y_2)=I(X_1,X_2;Y_1,Y_2)=I(X_1;Y_1)+I(X_2;Y_2)=2I(W)$$

所以$I(W^{-})+I(W^{+})=2I(W)$

对于极化子信道的互信息，利用链式法则，可以进一步展开为
$$\begin{array}{rl}I(W^{+})& =I(U_2;Y_1,Y_2,U_1)\\ & =I(U_2;Y_2)+I(U_2;Y_1,U_1|Y_2)\\ & =I(W)+I(U_2;Y_1,U_1|Y_2)\end{array}$$

因为$I(U_2;Y_1,U_1|Y_2)\ge 0$，因此$I(W^{+})\ge I(W)$，又因为$I(W^{-})+I(W^{+})=2I(W)$，所以必然有$I(W)\ge I(W^{-})$。
证毕！

由定理-1可知，两信道极化变换后的复合信道$(W^{-},W^{+})$的容量等于两个独立信道$W$的容量和，容量保持不变没有损失。

定理-2：对于两信道极化变换$(W,W)\mapsto (W^{-},W^{+})$，相应的极化子信道的巴氏参数满足：
$$\begin{array}{rl}Z(W^{+})& =Z^2(W)\\ Z(W^{-})& \le 2Z(W)-Z^2(W)\\ Z(W^{+})& \le Z(W)\le Z(W^{-})\end{array}$$

证明：略。

定理-2表明，经过两信道极化后，整个复合信道的可靠性得到了提升，巴氏参数满足如下关系
$$Z(W^{-})+Z(W^{+})\le 2Z(W)$$

当且仅当$W$是BEC信道时，等号成立。

小结
两信道极化是理解极化码的基础，经过简单的编码操作，构成了复合信道$(W^{-},W^{+})$，然后进一步分解为有相关性的两个极化子信道$W^{-}$和$W^{+}$，由定理-1可知，两信道和容量不发生变化，只是单个信道容量在两个极化子信道之间偏移，产生一好一差两极化分化。而由定理-2可知，两信道的巴氏参数和减小，意味着可靠性提升。

N信道极化的解释

长度为$N=2^n$的极化码是长度为2的极化码的扩展，即长度为2的极化码产生的极化信道$W_2^{(1)}$和$W_2^2$被当作另一个长度为2的极化码的$W$。一个长度为4的极化码的极化过程入下图所示，其中$(u_1,u_2,u_3,u_4)$是信源比特，$(x_1,x_2,x_3,x_4)$是码字比特。按照图中的走线，编码过程从左往右看，极化过程从右向左看

当$N=2$时，极化过程可以表示为$(W,W)\to (W_2^{(1)},W_2^{(2)})$，当$N=4$时，$(W_2^{(1)},W_2^{(1)})\to (W_4^{(1)},W_4^{(2)}),(W_2^{(2)},W_2^{(2)})\to (W_4^{(3)},W_4^{(4)})$

一般来讲，这个规律是：$(W_N^{(i)},W_N^{(i)})\to (W_{2N}^{(2i-1)},W_{2N}^{(2i)})$，其中$W_N^{(i)}$是长度为$N$的极化码的第$i$个极化信道，而$W_{2N}^{(2i-1)}$和$W_{2N}^{(2i)})$是长度为$2N$的极化码的第$(2i-1)$和$2i$个极化信道。

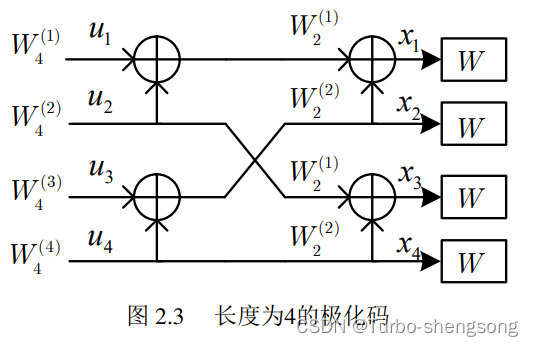
依照这个规律，一个长度为8的极化过程如下图所示，其中$(u_1,u_2,\cdots ,u_8)$是信源比特，$(x_1,x_2,\cdots ,x_8)$是码字比特。

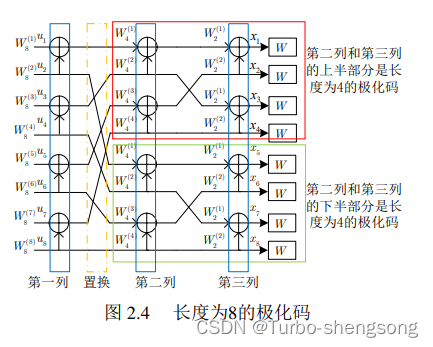
接下来，我们尝试寻找极化码编码过程或极化过程的通用描述，如上面两张图所示，由‘$\oplus$’和‘走线’构成的图称为长度为$N$的极化码的编码图，表示这张图的矩阵被称为生成矩阵${\mathbf{G}}_N$。当$N=2$时，生成矩阵${\mathbf{G}}_2=\mathbf{F}=\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]$.

我们参考【长度为8的极化码】进行解读。长度为$N$的极化码编码图的最左列是竖着排列的$\frac{N}{2}$个长度为2的极化码的编码图，所有这$\frac{N}{2}$个长度为2的极化码的第1个码字比特$(u_1\oplus u_2,u_3\oplus u_4,\cdots ,u_{N-1}\oplus u_N)$被置换到上一半，所有这$\frac{N}{2}$个长度为2的极化码的第2个码字比特$(u_2,u_4,\cdots ,u_N)$被置换到下一半。从左侧数【第2列至第n列】的 上半部分是要给长度为$\frac{N}{2}$的极化码的编码图（这就是极化码编码图的递归规律），写成矩阵乘法的形式为：
$${\mathbf{G}}_N=\left({\mathbf{I}}_{N/2}\otimes \mathbf{F}\right){\mathbf{R}}_N\left({\mathbf{I}}_2\otimes {\mathbf{G}}_{N/2}\right)$$

定义：极化码编码
长度为$N$的极化码的编码过程可以写为$GF(2)$上的矩阵乘法：
$${\mathbf{x}}_1^N={\mathbf{u}}_1^N{\mathbf{G}}_N$$

定义：极化信道
第$i$个信源比特$u_i$所经历的第$i$个极化信道具有如下的条件分布，这个条件分布表示为
$$\begin{array}{rl}{W}_N^{(i)}({\mathbf{y}}_1^N,{\mathbf{u}}_1^{i-1}|u_i)& =\text{Pr}({\mathbf{y}}_1^N,{\mathbf{u}}_1^i)/\text{Pr}(u_i)\\ & =2\sum _{u_{i+1}^N}\text{Pr}({\mathbf{y}}_1^N,{\mathbf{u}}_1^N)=\frac{2}{\text{Pr}({\mathbf{u}}_1^N)}\sum _{u_{i+1}^N}\text{Pr}({\mathbf{y}}_1^N|{\mathbf{u}}_1^N)\\ & =\frac{1}{2^{N-1}}\sum _{u_{i+1}^N}\text{Pr}({\mathbf{y}}_1^N|{\mathbf{x}}_1^N)\stackrel{(a)}{=}\frac{1}{2^{N-1}}\sum _{u_{i+1}^N}\prod _{i=1}^{N}W(y_i|x_i)\end{array}$$

其中${\mathbf{x}}_1^N={\mathbf{u}}_1^N{\mathbf{G}}_N$，等号(a)是因为信道$W$是无记忆的。上式中$W_N^{(i)}$表示概率集函数，相当于$\text{Pr}$，也用来代指第$i$个极化信道。如同转移概率$W(y|x)$的定义一样，信道$W_N^{(i)}({\mathbf{y}}_1^N,{\mathbf{u}}_1^{i-1}|u_i)$的【输入】是$u_i$，【输出】是${\mathbf{y}}_1^N$和${\mathbf{u}}_1^{i-1}$，即极化信道$W_N^i$不仅能观测到【物理信道$W$】的输出${\mathbf{y}}_1^N$，还能观测到比特值$(u_1,u_2,\cdots ,u_{i-1})$。这是因为极化码使用串行抵消译码，当从$u_1$开始逐一估计信源比特，直到$u_N$。因此，在译码$u_i$时，$(u_1,u_2,\cdots ,u_{i-1})$的值都已经获得，被当作译码$u_i$所需要的反馈。

定义：极化信道的递归关系
在长度为$N$的极化码中，极化信道具有如下的递归关系
$$\begin{array}{rl}{W}_N^{(2i-1)}({\mathbf{y}}_1^N,{\mathbf{u}}_1^{2i-2}|u_{2i-1})& =\frac{1}{2}\sum _{u_{2i}}{W}_{N/2}^{(i)}({\mathbf{y}}_1^{N/2},{\mathbf{u}}_{1,o}^{2i-2}\oplus {\mathbf{u}}_{1,e}^{2i-2}|u_{2i-1}\oplus u_{2i})W_{N/2}^{(i)}({\mathbf{y}}_{N/2+1}^N,{\mathbf{u}}_{1,e}^{2i-2}|u_{2i})\\ W_N^{(2i)}({\mathbf{y}}_1^N,{\mathbf{u}}_1^{2i-1}|u_{2i})& =\frac{1}{2}{W}_{N/2}^{(i)}({\mathbf{y}}_1^{N/2},{\mathbf{u}}_{1,o}^{2i-2}\oplus {\mathbf{u}}_{1,e}^{2i-2}|u_{2i-1}\oplus u_{2i})W_{N/2}^{(i)}({\mathbf{y}}_{N/2+1}^N,{\mathbf{u}}_{1,e}^{2i-2}|u_{2i})\end{array}$$

下面我们通过这张图，来进一步解释上面两个式子

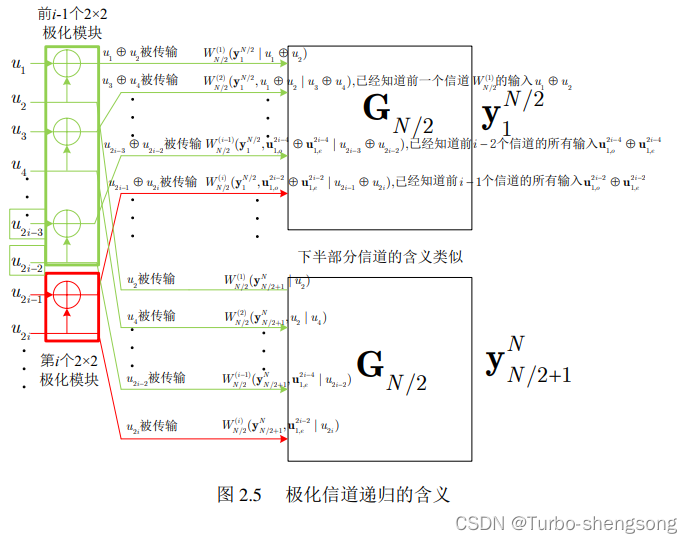
如果一个比特是$u_{2i-1}$，那么它必然和$u_{2i}$位于同一个2 x 2 极化模块的输入端。在极化码编码图的第一列中，$u_{2i-1}$和$u_{2i}$对应的2 x 2极化模块就是第$i$个极化模块。不难看出，$u_{2i-1}$和$u_{2i}$对应的2 x 2极化模块之前还有$i-1$个2 x 2极化模块，这些前面的极化模块对应的是$(u_1,u_2),\cdots ,(u_{2i-3},u_{2i-2})$

$u_{2i-1}$和$u_{2i}$对应的2 x 2极化模块右侧的两根走线分别连接到两个长度为$N/2$的极化码中的第$i$个极化信道，被连接的极化信道恰好都是长度为$N/2$的极化码中的第$i$个极化信道。$W_{N/2}^{(i)}({\mathbf{y}}_1^{N/2},{\mathbf{u}}_{1,o}^{2i-2}\oplus {\mathbf{u}}_{1,e}^{2i-2}|u_{2i-1}\oplus u_{2i})$能观测到${\mathbf{y}}_1^{N/2}$是显然的；还能观测到${\mathbf{u}}_{1,o}^{2i-2}\oplus {\mathbf{u}}_{1,e}^{2i-2}$也是显然的，因为$u_1\oplus u_2,u_3\oplus u_4,\cdots ,u_{2i-3}\oplus u_{2i-2}$由$u_{2i-1}$和$u_{2i}$对应的2 x 2极化模块之前的$i-1$个2 x 2极化模块所输送，注意到，极化码的串行抵消译码是序贯译码，在译码$u_{2i-1}$时，$u_1$和$u_{2i-2}$的值都已经获得，而${\mathbf{u}}_{1,o}^{2i-2}\oplus {\mathbf{u}}_{1,e}^{2i-2}$只不过是利用$u_1$至$u_{2i-2}$的值算出的结果而已；$W_{N/2}^{(i)}({\mathbf{y}}_1^{N/2},{\mathbf{u}}_{1,o}^{2i-2}\oplus {\mathbf{u}}_{1,e}^{2i-2}|u_{2i-1}\oplus u_{2i})$的输入为$u_{2i-1}\oplus u_{2i}$，这是因为$u_{2i-1}\oplus u_{2i}$对应的2 x 2极化模块将计算结果之一$u_{2i-1}\oplus u_{2i}$送入了该信道作为输入。

$W_{N/2}^{(i)}({\mathbf{y}}_{N/2+1}^N,{\mathbf{u}}_{1,e}^{2i-2}|u_{2i})$的含义按上一段类推，同理可得。

从而，把$W_{N/2}^{(i)}({\mathbf{y}}_1^{N/2},{\mathbf{u}}_{1,o}^{2i-2}\oplus {\mathbf{u}}_{1,e}^{2i-2}|u_{2i-1}\oplus u_{2i})$和$W_{N/2}^{(i)}({\mathbf{y}}_{N/2+1}^N,{\mathbf{u}}_{1,e}^{2i-2}|u_{2i})$视为$W$，把$u_{2i}$视为$u_2$，代入到2x2极化子信道$W^{-}:\mathcal{X}\to {\mathcal{Y}}^2$和$W^{+}:\mathcal{X}\to {\mathcal{Y}}^2\times \mathcal{X}$中，即可写出极化信道的递归关系。因此，N信道极化变换与两信道极化变换本质上是一一对应的。

信道极化分解的蝶形结构

我们以八信道极化分解为例，进行解释

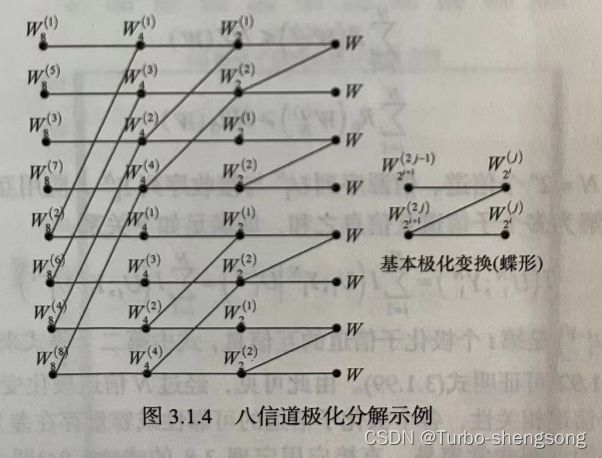
上图所示的极化分解包含了3级极化变换：
(1) 第一级：最右侧的8个独立信道$W$经过复合-分裂操作，得到【4组】独立的两信道极化集合 { W 2 ( 1 ) , W 2 ( 2 ) } \{W^{(1)}_2, W^{(2)}_2\} {W2(1)​,W2(2)​}
(2) 第二级：经过中间一级的极化变换，得到【两组】独立的四信道极化集合 { W 4 ( 1 ) , W 4 ( 2 ) , W 4 ( 3 ) , W 4 ( 4 ) } \{W^{(1)}_4, W^{(2)}_4, W^{(3)}_4, W^{(4)}_4\} {W4(1)​,W4(2)​,W4(3)​,W4(4)​}
(3) 第三级：经过左侧最后一级的极化变换，得到八信道极化集合 { W 8 ( 1 ) , W 8 ( 2 ) , W 8 ( 3 ) , W 8 ( 4 ) , W 8 ( 5 ) , W 8 ( 6 ) , W 8 ( 7 ) , W 8 ( 8 ) } \{W^{(1)}_8, W^{(2)}_8, W^{(3)}_8, W^{(4)}_8, W^{(5)}_8, W^{(6)}_8, W^{(7)}_8, W^{(8)}_8\} {W8(1)​,W8(2)​,W8(3)​,W8(4)​,W8(5)​,W8(6)​,W8(7)​,W8(8)​}

由此可见，$N=2^n$信道极化，应当包含${\log }_{2}N=n$级极化变换，每一级变换中，包含$N/2$个基本的【两信道极化变换】$(W_{2^i}^j,W_{2^i}^j)\mapsto (W_{2^{i+1}}^{2j-1},W_{2^{i+1}}^{2j})$，称为蝶形(Butterfly)结构。

补充：生成矩阵的结构

生成矩阵${\mathbf{G}}_N$可以表示为迭代形式
$${\mathbf{G}}_N=\left({\mathbf{I}}_{N/2}\otimes \mathbf{F}\right){\mathbf{R}}_N\left({\mathbf{I}}_2\otimes {\mathbf{G}}_{N/2}\right)$$

其对应的$N$信道极化的迭代过程为

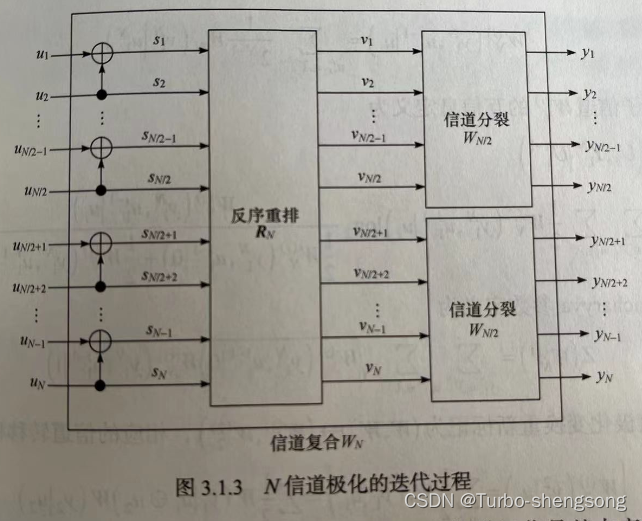
上述形式，在数学上也可以等价地写为第二种迭代形式
$${\mathbf{G}}_N={\mathbf{R}}_N({\mathbf{F}}_2\otimes {\mathbf{I}}_{N/2})({\mathbf{I}}_2\otimes {\mathbf{G}}_{N/2})={\mathbf{R}}_N({\mathbf{F}}_2\otimes {\mathbf{G}}_{N/2})$$

下图给出了该迭代式对应的N信道极化变换的迭代过程

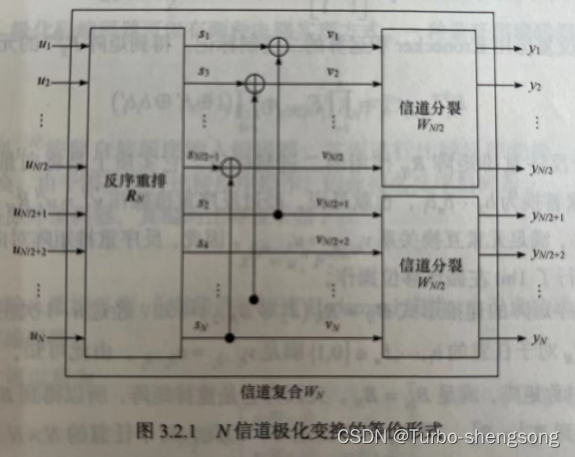
将递归形式${\mathbf{G}}_{N/2}={\mathbf{R}}_{N/2}({\mathbf{F}}_2\otimes {\mathbf{G}}_{N/4})$代入到迭代式中，利用等式$\mathbf{AC}\otimes \mathbf{BD}=\mathbf{AB}\otimes \mathbf{CD}$，可以得到
$${\mathbf{G}}_N={\mathbf{R}}_N\left({\mathbf{F}}_2\otimes \left({\mathbf{R}}_{N/2}({\mathbf{F}}_2\otimes {\mathbf{G}}_{N/4})\right)\right)={\mathbf{R}}_N\left({\mathbf{I}}_2\otimes {\mathbf{R}}_{N/2}\right)\left({\mathbf{F}}_2^2\otimes {\mathbf{G}}_{N/4}\right)$$

重复上述过程，最终得到
$${\mathbf{G}}_N={\mathbf{B}}_N{\mathbf{F}}_2^{\otimes n}$$

其中${\mathbf{B}}_N={\mathbf{R}}_N({\mathbf{I}}_2\otimes {\mathbf{R}}_{N/2})({\mathbf{I}}_4\otimes {\mathbf{R}}_{N/4})\cdots ({\mathbf{I}}_{N/2}\otimes {\mathbf{R}}_2)$是比特反序矩阵，基于迭代结构，比特反序 矩阵也可以表示为递推形式
$${\mathbf{B}}_N={\mathbf{R}}_N({\mathbf{I}}_2\otimes {\mathbf{B}}_{N/2})$$

其初始条件${\mathbf{B}}_2={\mathbf{I}}_2$。

参考文献
[1] E. Arikan, “Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels,” in IEEE Transactions on Information Theory, vol. 55, no. 7, pp. 3051-3073, July 2009, doi: 10.1109/TIT.2009.2021379.
[2] 牛凯. 极化码原理与应用. Print.(2021)
[3] 于永润. 极化码讲义.